时域法提供了一种简单直观的方式分析线性系统闭环传递函数的零、极点对系统性能产生的影响。但是,对于高阶系统,即使用拉普拉斯变换将系统微分方程变换为 的高阶代数方程,在没有现代计算机方法的情况下求解依然十分困难,并且难以求得系统参数(如开环增益 $K$)变化对系统带来的影响。
1948年,美国工程师 Walter R. Evans 提出了根轨迹法,通过在改变系统参数时绘制出 $s$ 平面上系统闭环特征方程的根的移动轨迹,可以方便地获知在参数变化时系统稳定性与动态性能指标,并选择合适的参数。相比时域法,根轨迹法计算量小、使用简单,在控制工程中获得了广泛的应用。
根轨迹的基本概念
根轨迹是当开环系统某一参数(如根轨迹增益 $K^\ast$)从零变化到无穷大时,闭环特征方程的根在 $s$ 平面上移动的轨迹。 根轨迹增益 $K^\ast$ 是首 $1$ 形式开环传递函数对应的系数。
以下图所示的一个系统为例:

控制系统结构图(109页 图4-1)
这是一个单位反馈系统,其开环传递函数 $G(s) = \dfrac{K}{s (0.5s + 1)} = \dfrac{K^\ast}{s (s + 2)} = \dfrac{M(s)}{N(s)} \ ,$ 根轨迹增益 $K^\ast = 2 K \ .$
这个系统的闭环特征方程为
$$D(s) = M(s) + N(s) = s^2 + 2s + K^\ast \ ,$$
解得特征根
$$\lambda_{1, 2} = -1 \pm \sqrt{1 - K^\ast} \ .$$
现在我们绘制一个 $s$ 平面,并考虑改变 $K$ 时,$\lambda_1, \lambda_2$ 会如何分布在 $s$ 平面上。由于我们研究的是一个物理可实现的系统,故 $K$ 的值应当从 $0$ 开始。
当 $0 < K < 0.5$ 时,$1 - K > 0 \ ,$ 此时 $\lambda_1, \lambda_2$ 都为实数,并且分别从 $\lambda_1 = 0$ 与 $\lambda_2 = -1$ 点开始向 $(-0.5, \mathrm{j} 0)$ 点汇聚;
当 $K = 0.5$ 时, $\lambda_1, \lambda_2$ 在 $(-0.5, \mathrm{j} 0)$ 点处重叠;
当 $K > 0.5$ 时, $1 - K < 0 \ ,$ 此时 $\lambda_1, \lambda_2$ 开始具有虚部,进入 $s$ 平面上;由于此时实部 $-1$ 不再改变, $K$ 只影响虚部,故 $\lambda_1, \lambda_2$ 会在 $\mathrm{Re}(s) = -1$ 直线上随着 $K$ 的增大相背而行,直至 $-1 \pm \mathrm{j} \infty \ .$
根据上面的讨论,我们可以绘制出系统的根轨迹图如下。

系统根轨迹图(110页 图4-2)
根轨迹与系统性能
在上一篇文章 自动控制原理 - 03 - 线性控制系统的时域分析 中,我们详细讨论了系统闭环特征根对性能的影响,尤其是二阶系统在无阻尼振荡频率 $\omega_\mathrm{n}$ 与阻尼比 $\zeta$ 改变时的性能变化;当以极坐标表示时,$\omega_\mathrm{n}$ 控制极点的模长,$\zeta$ 控制极点的相角(以负实轴顺时针计)。下面我们将以刚刚的系统为例讨论开环增益 $K$ 取不同值时,对应系统特征根在 $s$ 平面上的移动会如何影响系统性能。
稳定性
回顾上篇文章的 线性系统的稳定性分析 一节:
先给出结论:对于从系统特征方程 $D(s) = 0$ 解得的特征根,无论是实根还是共轭复根,所有特征根都具有负的实部是系统稳定的充分必要条件。
换句话说,稳定系统的所有闭环特征根都应当在 $s$ 平面虚轴左侧。观察上面的系统不难发现当 $K > 0$ 时,其所有闭环特征根构成的轨迹都在 $s$ 平面左半边,故系统总是稳定的。
对于其他类型的系统,根轨迹有时不会局限于 $s$ 平面左半边,而是以复杂轨迹越过虚轴进入虚轴右侧。此时在相应 $K$ 值下系统存在具有正实部的闭环特征根,从而是不稳定的;而当闭环特征根恰好在虚轴上时,系统处于临界稳定状态,以二阶系统为例就是阻尼比 $\zeta = 0$ 时系统具有两个纯虚特征根,其时域响应呈等幅振荡状态。
稳态性能
由上图可知系统在坐标原点处存在一开环极点,系统属于 $\mathrm{I}$ 型系统,开环增益 $K$ 等于静态速度误差系数 $K_\mathrm{v} \ .$
当 $r(t) = 1(t)$ 时,$e_\mathrm{ss} = 0 \ ;$
当 $r(t) = A t$ 时,$e_\mathrm{ss} = \dfrac{A}{K} = \dfrac{2A}{K^\ast} \ .$
动态性能
对于刚刚举例的二阶系统,其根轨迹上根的位置对系统动态性能的影响完全满足我们之前在 二阶系统的时域分析 讨论过的内容:
当 $0 < K < 0.5$ 时,闭环特征根为实根,系统呈现过阻尼状态,阶跃响应为单调上升过程;
当 $K = 0.5$ 时,闭环特征根为二重实根,系统呈现临界阻尼状态,阶跃响应仍为单调过程,但响应速度较 $0 < K < 0.5$ 时为快;
当 $K > 0.5$ 时,闭环特征根为一对共轭复根,系统呈现欠阻尼状态,阶跃响应为振荡衰减过程,且随 $K$ 增加,阻尼比减小,超调量增大,但 $t_s$ 基本不变1。
由以上讨论我们可以看出,根轨迹与系统性能之间有着密切的联系,利用根轨迹可以分析当系统参数(如 $K$ 或 $K^\ast$)增大时系统动态性能的变化趋势。
闭环零极点与开环零极点的关系
考虑下图(a)所示的典型系统。
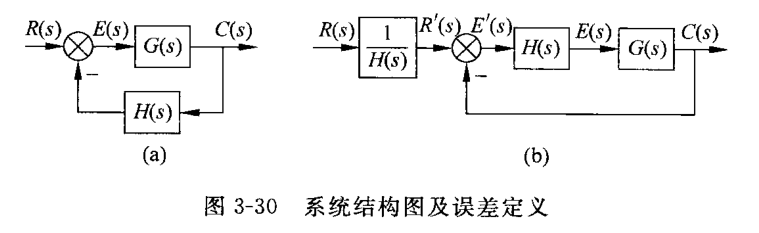
典型系统结构图(85页 图3-30)
假设其有 $m$ 个开环零点、$n$ 个开环极点,则
$$ G(s) = \frac{K_\mathrm{G}^\ast \displaystyle \prod_{i=1}^{f} (s - z_i)}{\displaystyle \prod_{i=1}^{g} (s - p_i)}, \qquad H(s) = \frac{K_\mathrm{H}^\ast \displaystyle \prod_{j=f+1}^{m} (s - z_j)}{\displaystyle \prod_{j=g+1}^{g} (s - p_j)} $$
注意看各个 $\prod$ 的上限:$G(s)$ 中有 $f$ 个开环零点与 $g$ 个开环极点,相应地 $H(s)$ 中有 $m-f$ 个开环零点与 $n-g$ 个开环极点。于是此系统的开环传递函数
$$ G(s)H(s) = \frac{K^\ast \displaystyle \prod_{i=1}^{f} (s - z_i) \displaystyle \prod_{j=f+1}^{m} (s - z_j)}{\displaystyle \prod_{i=1}^{g} (s - p_i) \displaystyle \prod_{j=g+1}^{g} (s - p_j)} = \frac{K^\ast \displaystyle \prod_{i=1}^{m} (s - z_i)}{\displaystyle \prod_{j=1}^{n} (s - p_j)} \ , $$
式中 $K^\ast = K_\mathrm{G}^\ast K_\mathrm{H}^\ast$ 为系统的根轨迹增益,$z_i$ 表示开环零点,$p_j$ 表示开环极点。系统闭环传递函数为
$$ \varPhi(s) = \frac{1}{1 + G(s) H(s)} = \frac{K^\ast \displaystyle \prod_{i=1}^{f} (s - z_i) \displaystyle \prod_{j=g+1}^{g} (s - p_j)}{\displaystyle \prod_{j=1}^{n} (s - p_j) + K^\ast \displaystyle \prod_{i=1}^{m} (s - z_i)} $$
从上式可知:
闭环零点由前向通路传递函数 $G(s)$ 的零点和反馈通路传递函数 $H(s)$ 的极点组成。 对于单位反馈系统 $H(s) = 1 \ ,$ 闭环零点就是开环零点。闭环零点不随 $K^\ast$ 变化,不必专门讨论之。
闭环极点与开环零点、开环极点以及根轨迹增益 $K^\ast$ 均有关。 闭环极点随 $K^\ast$ 而变化,所以研究闭环极点随 $K^\ast$ 的变化规律是必要的。
欠阻尼二阶系统的 $t_s \approx \frac{3.5}{\zeta \omega_\mathrm{n}} = \frac{3.5}{\omega_\mathrm{d}}\ ,$ 即只和共轭复根的实部有关;此处系统的特征根实部不变,之所以说“$t_s$ 基本不变”是因为上式为估算值,与实际值多少有些误差。 ↩︎