从本篇文章开始我们将正式进入控制系统的分析与校正。从时域上对控制系统进行分析符合人类直觉,比起根轨迹法和频域法更有“看得见、摸得着”的感觉;但时域法在对系统参数进行调整以使性能指标朝我们希望的方向进行改变,即系统校正上有所欠缺。即使如此,我们在学习时域法时会接触到许多基本的概念、方法和结论,对后续的控制理论学习都有很大帮助。
时域法常用的典型输入信号与性能指标
典型输入信号
在时域分析中,我们一般会用到这些典型输入信号:
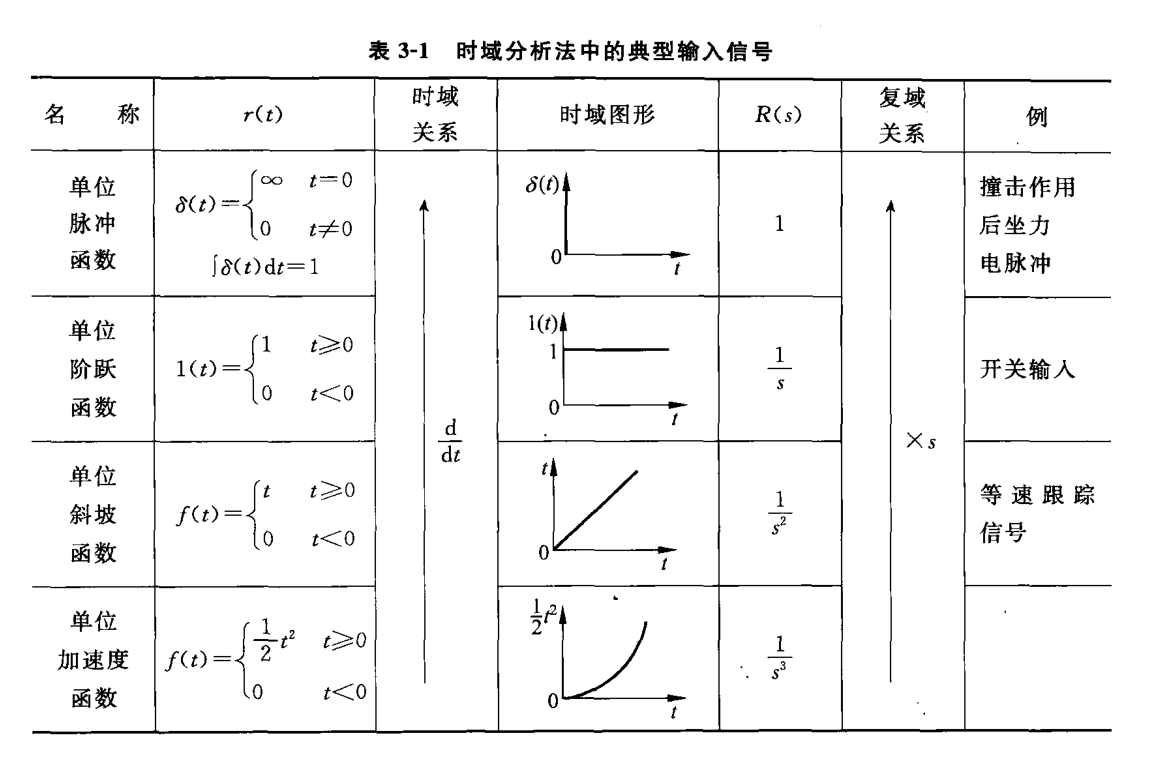
时域分析法中的典型输入信号(54页 表3-1)
单位脉冲函数 $\delta(t)$:得到的响应即为系统的闭环传递函数。
单位阶跃函数 $1(t)$:又称为位置输入,是工程上最常用的输入信号。由于单位阶跃输入容易实现、对系统的要求比较高(具有陡峭的信号突变,且在 $t > 0$ 时始终存在输入),故后续的时域分析多以单位阶跃为输入信号展开研究。
性能指标
这部分内容来自卢京潮《自动控制原理》第3章 线性系统的时域分析与校正 3.1.3 系统的常用时域性能指标。
动态性能指标
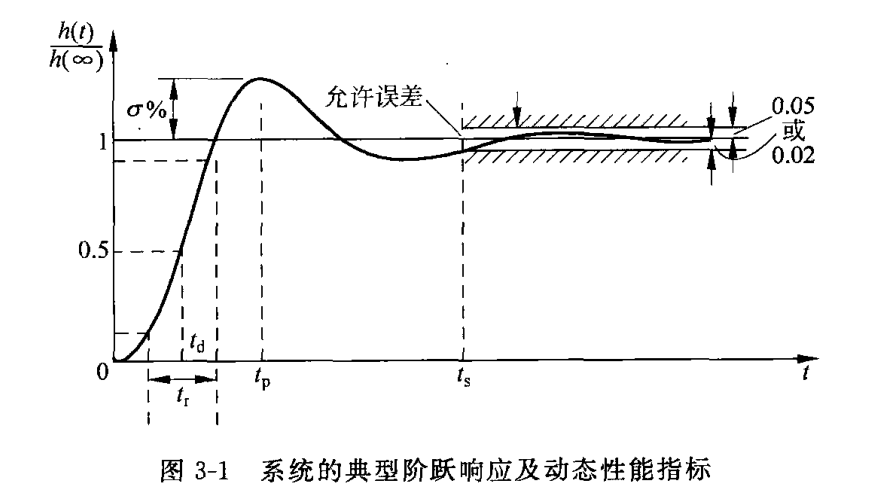
系统的典型阶跃响应及动态性能指标(54页 图3-1)
上表是以典型欠阻尼二阶系统的阶跃响应为基础绘制的。当衡量系统的动态性能时,我们一般使用这些指标:
上升 (raise) 时间 $t_r$: 阶跃响应从终值的 $10 \char37$ 上升到终值的 $90 \char37$ 所需的时间;对有振荡的系统,也可定义为从0到第一次达到终值所需的时间。
峰值 (peak) 时间 $t_\mathrm{p}$: 阶跃响应越过终值 $h(\infin)$ 达到第一个峰值所需的时间。
调节 (settling) 时间 $t_\mathrm{s}$: 阶跃响应到达并保持在终值$h(\infin) \pm 5 \char37$ 误差带内所需的最短时间;有时也用终值的 $\pm 2 \char37$ 误差带来定义调节时间。在卢老师的课程中,一般均以终值的 $\pm 5 \char37$ 误差带定义调节时间。
超调 (overshoot) 量 $\sigma \char37$: 峰值 $h(t_\mathrm{p})$ 超出终值 $h(\infin)$ 的百分比,即
$$\sigma \char37 = \frac{h(t_\mathrm{p}) - h(\infin)}{h(\infin)} \times 100 \char37$$
- 延迟 (delay) 时间 $t_d$: 阶跃响应第一次达到终值 $h(\infin)$ 的 $50 \char37$ 所需的时间。
在上述动态性能指标中,工程上最常用的是调节时间 $t_\mathrm{s}$(反映过渡过程的长短,描述 “快”),超调量$\sigma \char37$(反映过渡过程的波动程度,描述“匀”)以及峰值时间 $t_\mathrm{p}$.
稳态性能指标
当我们考虑系统的稳态性能时,实际上我们研究的是系统在达到稳态的情况下,其输出与我们所期望的输出之差值,称为系统的稳态误差。用更精确的语言进行表述:稳态误差是时间趋于无穷时系统实际输出与理想输出之间的误差,是系统控制精度或抗干扰能力的一种度量。
应当指出,系统性能指标的确定应根据实际情况而有所侧重。例如,民航客机要求飞行平稳,不允许有超调;歼击机则要求机动灵活,响应迅速,允许有适当的超调;对于一些启动之后便需要长期运行的生产过程(如化工过程等)则往往更强调稳态精度。
一阶系统的时域分析
一阶系统的时域分析相对比较简单。我们可以从系统的典型结构图出发进行分析:

一阶系统典型结构图(55页 图3-2)
系统的传递函数为
$$\varPhi(s) = \frac{K}{s + K} = \frac{1}{Ts+1}\ ,$$
可以解得系统特征根1 $\lambda = -\dfrac{1}{T} \ .$
上式中 $T=\dfrac{1}{K}$ 称为一阶系统的时间常数,在分析一阶系统时有重要意义。
对于一阶系统,在复频域上计算其单位阶跃响应为
$$ C(s) = \mathit{\Phi (s)} \cdot R(s) = \frac{1}{Ts+1} \frac{1}{s} = \frac{1}{s} - \frac{1}{s + \frac{1}{T}} \ , $$
通过拉普拉斯变换即得到时域响应
$$h(t) = \mathscr{L}^{-1}[C(s)] = 1-\mathrm{e}^{- \frac{t}{T}} .$$
一阶系统的动态性能指标
一阶系统的单位阶跃响应如下图所示,是一条单调的指数上升曲线。
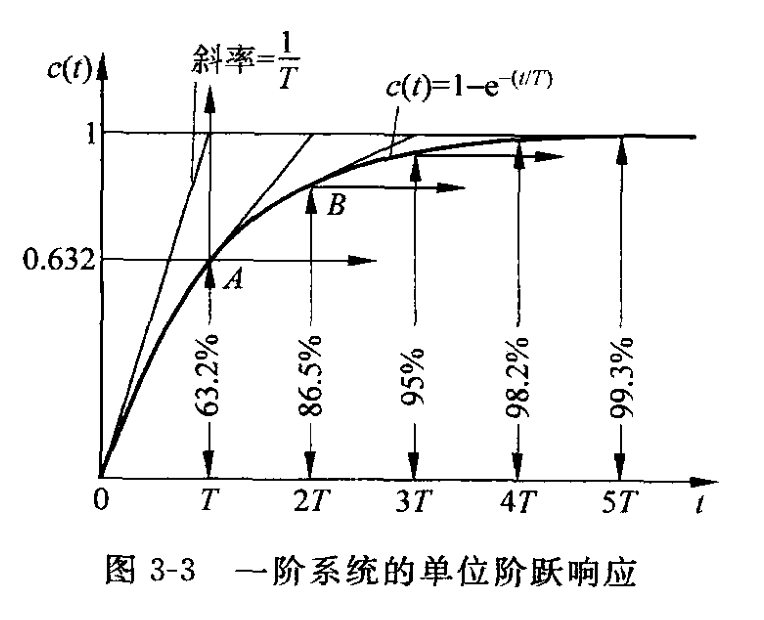
一阶系统的单位阶跃响应(56页 图3-3)
由调节时间 $t_\mathrm{s}$ 的定义可得
$$h(t_\mathrm{s}) = 1 - \mathrm{e}^{\frac{t_\mathrm{s}}{T}} = 0.95 \ ,$$
可以解得
$$t_\mathrm{s} = 2.9957T \approx 3T \ .$$
从上图也可以验证这个结论。图3-3表明,可以用时间常数 $T$ 描述一阶系统的响应特性。时间常数 $T$ 是一阶系统的重要特征参数。$T$ 越小,系统极点越远离虚轴,过渡过程越快2。
类似地,可以讨论一阶系统的脉冲响应和斜坡响应,并将一阶系统对不同典型信号的响应汇总如下:
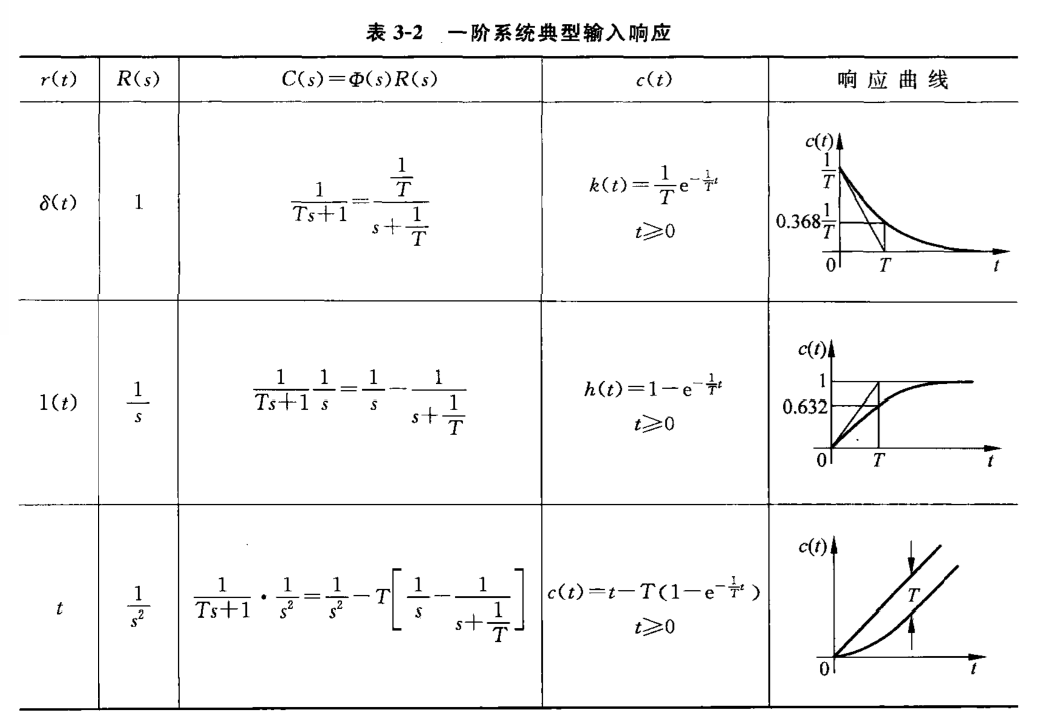
一阶系统典型输入响应(56页 表3-2)
从表中容易看出,系统对某一输入信号的微分/积分的响应,等于系统对该输入信号响应的微分/积分。 这是线性定常系统的重要性质,对任意阶线性定常系统均适用。
二阶系统的时域分析
这部分内容基本来自于卢京潮《自动控制原理》第3章 线性系统的时域分析与校正 3.3 二阶系统的时间响应及动态性能。
二阶系统分析是本章的重点。相比一阶系统,二阶系统引入的额外极点会使得系统不再稳定地趋于收敛,而是依阻尼比不同产生震荡甚至发散;下面我们来详细讨论这一点。
典型的二阶系统结构图如图3-6 (a)所示,其中 $K, T_0$ 为环节参数。
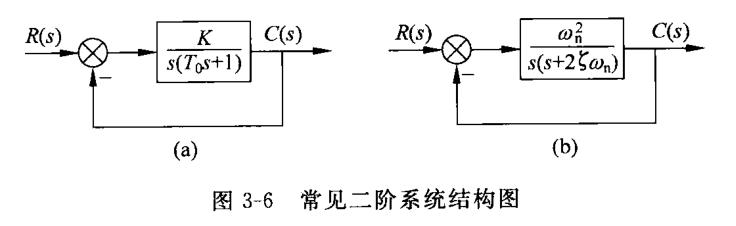
常见二阶系统结构图(58页 表3-6)
系统的闭环传递函数为
$$\varPhi (s) = \frac{K}{T_0 s^2 + s + K} \ ,$$
化为标准形式
$$ \begin{aligned} \varPhi(s) &= \frac{\omega_\mathrm{n}^2}{s^2 + 2\zeta\omega s + \omega_\mathrm{n}^2} &\qquad& (\text{首1型}) \newline \newline \varPhi(s) &= \frac{K}{T_0 s^2 + s + K} &\qquad& (\text{尾1型}) \end{aligned} $$
式中 $\displaystyle T = \sqrt{\frac{T_0}{K}}, \quad \omega_\mathrm{n} = \frac{1}{T} = \sqrt{\frac{K}{T_0}}, \quad \zeta = \frac{1}{2} \sqrt{\frac{1}{K T_0}} \quad .$
以上的 $\zeta, \omega_\mathrm{n}$ 分别称为系统的阻尼比和无阻尼自然频率,是二阶系统重要的特征参数。二阶系统的首1标准型传递函数常用于时域分析中,频域分析时则常用尾1标准型。
二阶系统闭环特征方程为
$$D(s) = s^2 + 2\zeta\omega_\mathrm{n} s + \omega_\mathrm{n}^2 = 0 \ ,$$
对应的特征根为
$$\lambda_{1, 2} = -\zeta \omega_\mathrm{n} \pm \mathrm{j} \omega_\mathrm{n} \sqrt{1 - \zeta^2} \qquad (0 < \zeta < 1),$$
上式为欠阻尼情况的系统特征根。一般可以根据阻尼比 $\zeta$ 的不同,将二阶系统区分为零阻尼,欠阻尼,临界阻尼和过阻尼系统;当改变 $\zeta$ 时,二阶系统的特征根在 $s$ 平面上的分布随之改变,系统特性会有比较明显的变化。我们将在后面讨论这一点。

二阶系统(按阻尼比 $\zeta$ )分类表(59页 表3-3)
欠阻尼二阶系统的动态过程分析
一般教材都会先介绍过阻尼和临界阻尼的二阶系统分析,再来用长篇幅介绍欠阻尼的情况;但作为复习,我们先研究欠阻尼二阶系统是如何分析的,再考虑临界阻尼和过阻尼这样的特殊情况。
当二阶系统阻尼比参数 $0 < \zeta < 1$ 时,我们称这个二阶系统处于欠阻尼状态。
先来看一张重要的图:
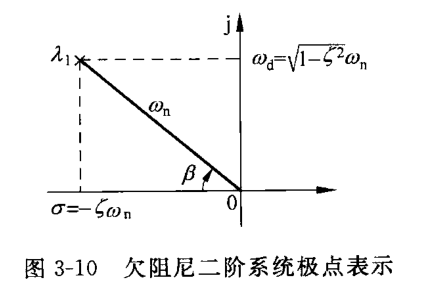
欠阻尼二阶系统的极点表示(62页 图3-10)
我们刚刚分析了二阶系统的闭环特征方程并解出了一对共轭的特征根。参照上图可以看到,欠阻尼二阶系统的特征根总是在 $s$ 平面的虚轴左侧(即具有负实部),其中
$\sigma = \zeta \omega_\mathrm{n}$: 衰减系数,决定了系统单位阶跃响应收敛的速度;
$\omega_d = \omega_\mathrm{n} \sqrt{1 - \zeta^2}$: 有阻尼振荡频率;
$\omega_\mathrm{n}$: 无阻尼振荡频率,是系统的固有特性参数,若令 $\zeta = 0$ 并保持其他参数不变,系统将会做频率为 $\omega_\mathrm{n}$ 的等幅正弦振荡。
$\beta$: 阻尼角,在后续的根轨迹分析/频率域分析中有重要作用。
欠阻尼二阶系统的单位阶跃响应
对于欠阻尼二阶系统,其单位阶跃响应的拉普拉斯变换为
$$ \begin{aligned} C(s) &= \varPhi(s) R(s) = \frac{\omega_\mathrm{n}^2}{s^2 + 2 \zeta \omega_\mathrm{n} s + \omega_\mathrm{n}^2} \frac{1}{s} = \frac{1}{s} - \frac{s + 2 \zeta \omega_\mathrm{n}}{(s + \zeta \omega_\mathrm{n})^2 + (1 - \zeta^2) \omega_\mathrm{n}^2} \newline &= \frac{1}{s} - \frac{s + \zeta \omega_\mathrm{n}}{(s + \zeta \omega_\mathrm{n})^2 + (1 - \zeta^2) \omega_\mathrm{n}^2} - \frac{\zeta}{\sqrt{1 - \zeta^2}} \cdot \frac{\sqrt{1 - \zeta^2} \omega_\mathrm{n}}{(s + \zeta \omega_\mathrm{n})^2 + (1 - \zeta^2) \omega_\mathrm{n}^2} \end{aligned} \ , $$
反变换得到时域的阶跃响应3
$$ \begin{aligned} h(t) &= 1 - \mathrm{e}^{-\zeta \omega_\mathrm{n} t} \cos(\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) - \frac{\zeta}{\sqrt{1 - \zeta^2}} \mathrm{e}^{-\zeta \omega_\mathrm{n} t} \sin(\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) \newline &= 1 - \frac{\mathrm{e}^{-\zeta \omega_\mathrm{n} t}}{\sqrt{1 - \zeta^2}} \left [ \sqrt{1 - \zeta^2} \cos(\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) - \frac{\zeta}{\sqrt{1 - \zeta^2}} + \zeta \sin(\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) \right ] \newline &= 1 - \frac{\mathrm{e}^{-\zeta \omega_\mathrm{n} t}}{\sqrt{1 - \zeta^2}} \sin \left ( \sqrt{1 - \zeta^2} \omega_\mathrm{n} t + \arctan \frac{\sqrt{1 - \zeta^2}}{\zeta} \right ) \newline &= 1 - \frac{\mathrm{e}^{-\sigma t} }{\sin \beta} \sin \left ( \omega_d t + \beta \right ) \ , \end{aligned} $$
当改变阻尼比 $\zeta$ 时,时域响应也随之变化如下:
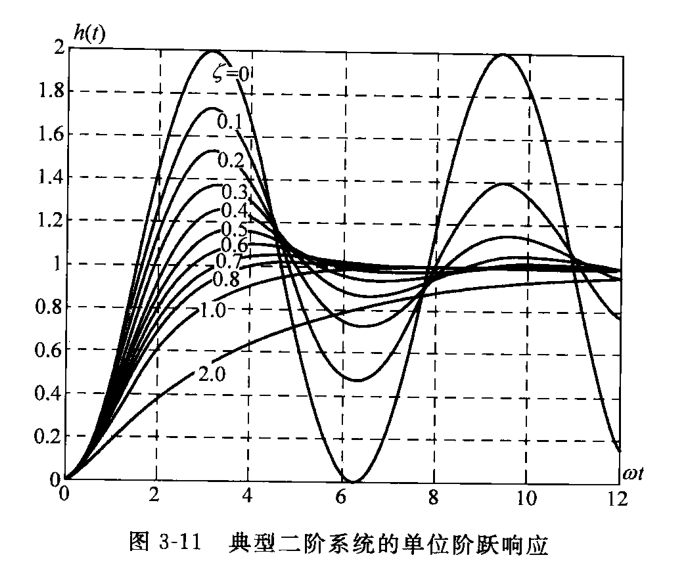
典型二阶系统的单位阶跃响应(63页 图3-11)
回到刚刚 欠阻尼二阶系统的极点表示 这张图。从系统时域单位阶跃响应的公式中我们可以看出,欠阻尼二阶系统的单位阶跃响应由两部分组成:稳态分量为 $1 \ ,$ 表明系统在单位阶跃函数作用下不存在稳态位置误差;瞬态分量为阻尼正弦振荡项,故其振荡频率为 $\omega_\mathrm{n}$ 称为阻尼振荡频率。由于瞬态分量衰减的快慢程度取决于包络线 $1 \pm \frac{1}{\sqrt{1 - \zeta^2} } \mathrm{e}^{-\zeta \omega_\mathrm{n} t}$ 收敛的速度,当 $\zeta$ 一定时,包络线的收敛速度又取决于指数函数 $\mathrm{e}^{-\zeta \omega_\mathrm{n} t}$ 的幂,所以 $\sigma = \zeta \omega_\mathrm{n}$ 称为衰减系数。
系统单位阶跃响应的初始值 $h(0) = 0 \ ,$ 初始斜率 $h^\prime (0) = 0 \ ,$ 终值 $h(\infin) = 1 \ .$
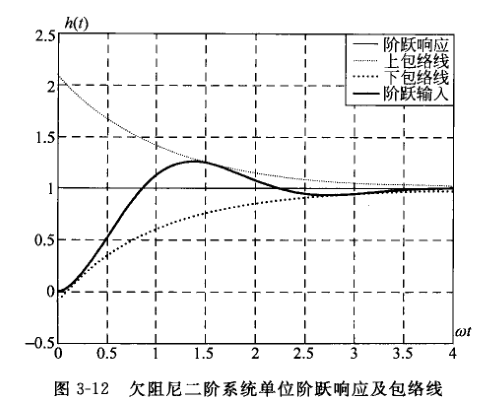
欠阻尼二阶系统单位阶跃响应及包络线(63页 图3-12)
二阶系统的单位脉冲响应为
$$ \begin{aligned} k(t) &= h^\prime (t) = \mathscr{L}^{-1} \left [ \frac{\omega_\mathrm{n}}{\sqrt{1 - \zeta^2}} \cdot \frac{\sqrt{1 - \zeta^2} \omega_\mathrm{n}}{(s + \zeta \omega_\mathrm{n})^2 + (1 - \zeta^2) \omega_\mathrm{n}^2} \right] \newline &= \frac{\omega_\mathrm{n}}{\sqrt{1 - \zeta^2}} \mathrm{e}^{-\zeta \omega_\mathrm{n} t} \sin(\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) \newline &= \frac{\omega_\mathrm{n}}{\sin \beta} \mathrm{e}^{-\sigma t} \sin(\omega_d t) \ . \end{aligned} $$
欠阻尼二阶系统的动态性能指标
峰值时间 $t_\mathrm{p}$
令 $h^\prime (t) = k(t) = 0$ 可得方程
$$\sin (\sqrt{1 - \zeta^2} \omega_\mathrm{n} t) = 0 \ ,$$
即
$$\sqrt{1 - \zeta^2} \omega_\mathrm{n} t = 0, \pi, 2 \pi, 3 \pi, …$$
峰值时间指的是第一次达到峰值使 $h^\prime (t) = 0$ 的时刻,故取上式右边为 $\pi$ 可得欠阻尼二阶系统的峰值时间计算公式
$$t_\mathrm{p} = \frac{\pi}{\sqrt{1 - \zeta^2} \omega_\mathrm{n} } = \frac{\pi}{\omega_\mathrm{d} } \ ,$$
超调量 $\sigma \char37$
将峰值时间 $t_\mathrm{p}$ 代入系统单位阶跃响应的计算公式可得
$$ \begin{aligned} h(t_\mathrm{p}) &=1 - \frac{\mathrm{e}^{-\zeta \omega_\mathrm{n} \frac{\pi}{\sqrt{1 - \zeta^2} \omega_\mathrm{n} }}}{\sqrt{1 - \zeta^2}} \sin \left ( \sqrt{1 - \zeta^2} \omega_\mathrm{n} \frac{\pi}{\sqrt{1 - \zeta^2} \omega_\mathrm{n} } + \arctan \frac{\sqrt{1 - \zeta^2}}{\zeta} \right ) \newline &= 1 + \mathrm{e}^{-\frac{\zeta \pi}{\sqrt{1 - \zeta^2}}} \newline &= 1 + \mathrm{e}^{-\pi \cot \beta} \ , \end{aligned} $$
从而可求得超调量
$$\sigma \char37 = \frac{h(t_\mathrm{p}) - h(\infin)}{h(\infin)} \times 100 \char37 = \mathrm{e}^{-\pi \cot{\beta}} \times 100 \char37 \ ,$$
从上式可知典型欠阻尼二阶系统的超调量 $\sigma \char37$ 只与阻尼比 $\zeta$ 有关。
调节时间 $t_\mathrm{s}$
用定义求解调节时间相对来说是比较麻烦的。但从 刚刚的讨论 中我们了解到,欠阻尼二阶系统的阶跃响应总是被包围在一对包络线中,实际响应的各时刻的幅值都不会超过对应的包络线;因此,我们可以以包络线进入 $2 \char37$ 或 $5 \char37$ 误差带的时间估算系统调节时间。这种方法所求得的调节时间略保守,但相对来说计算简便,为工程计算所采用。
按调节时间定义列出包络线所满足的方程,可得
$$\left | 1 + \frac{1}{\sqrt{1 - \zeta^2}} \mathrm{e}^{-\zeta \omega_\mathrm{n} t} - 1\right | = \frac{1}{\sqrt{1 - \zeta^2}} \mathrm{e}^{-\zeta \omega_\mathrm{n} t} = 0.05 \ ,$$
解得
$$t_\mathrm{p} = - \dfrac{\ln 0.05 + \frac{1}{2} \ln{ (1 - \zeta^2)} }{\zeta \omega_\mathrm{n} } \approx \dfrac{3.5}{\zeta \omega_\mathrm{n} } \qquad \qquad \left ( 0.3 < \zeta < 0.8 \right ) \ ,$$
可以用此式估算系统在取 $5 \char37$ 误差带时的调节时间。此外,当取 $2 \char37$ 误差带时,调节时间的计算公式为
$$t_\mathrm{p} = \dfrac{4.4}{\zeta \omega_\mathrm{n} } \ .$$
典型欠阻尼二阶系统动态性能、系统参数与极点分布之间的关系
有关系统参数对极点及动态性能的影响,在根轨迹和频域分析中会更为明显,此处仅作简单地定性分析。
由于我们刚刚对调节时间 $t_\mathrm{s}$ 的计算是通过包络线估算的,实际上当 $\zeta \omega_\mathrm{n}$ 一定时, $t_\mathrm{s}$ 还会随着阻尼比 $\zeta$ 的变化而变化。当 $\zeta = 0.707$ 时, $t_\mathrm{s} \approx 2T \ ,$ 实际调节时间最短,且此时超调量 $\sigma \char37 = 4.32 \char37 \approx 5 \char37$ 也比较小,故一般称 $\zeta = 0.707$ 为“最佳阻尼比”。
再次回顾二阶系统的特征根表达式
$$\lambda_{1, 2} = -\zeta \omega_\mathrm{n} \pm \mathrm{j} \omega_\mathrm{n} \sqrt{1 - \zeta^2} \qquad (0 < \zeta < 1),$$
与极点坐标对应的各个参数

欠阻尼二阶系统的极点表示(62页 图3-10)
由于二阶系统的极点是共轭的,因此我们这里以上半平面(虚部为正)的极点为对象展开分析,与其关于实轴镜像对称的共轭极点也有类似的行为。
当 $\omega_\mathrm{n}$ 不变,增加 $\zeta$ 时,极点的阻尼角 $\beta$ 减小,系统极点将在 $s$ 平面的左半部分的以 $\omega_\mathrm{n}$ 为半径的圆弧上逆时针运动,并对应系统超调量 $\sigma \char37$ 减小;同时此过程中极点逐渐远离虚轴,$\zeta \omega_\mathrm{n}$ 增加,调节时间 $t_\mathrm{s}$ 减小。下图(a)给出了 $\omega_\mathrm{n} = 1 \ , \zeta$ 发生变化时的系统单位阶跃响应过程。
当 $\zeta$ 固定,增加 $\omega_\mathrm{n}$ 时,极点的阻尼角 $\beta$ 不变,从极坐标角度考虑系统极点将在 $s$ 平面上一条射线上移动,并对应系统超调量 $\sigma \char37$ 不变;同时此过程中极点也会远离虚轴, $\zeta \omega_\mathrm{n}$ 增加,调节时间 $t_\mathrm{s}$ 减小。下图(b)给出了 $\zeta = 0.5 (\beta = 60\degree), \omega_\mathrm{n}$ 发生变化时的系统单位阶跃响应过程。
一般实际系统中(如 图3-6 所示)的 $T_0$ 是系统的固定参数,不能随意改变;而开环增益 $K$ 是各环节总的传递系数,可以调节。 $K$ 变化时,$\zeta \omega_\mathrm{n} = \frac{1}{T_0}$ 保持不变,即极点的实部不改变,在与虚轴平行的一条直线上移动;随着 $K$ 增大,系统的阻尼角 $\beta$ 增加,对应阻尼比 $\zeta$ 变小,超调量 $\sigma \char37$ 增加。下图(c)给出了 $T_0 = 1, \ K$ 发生变化时系统单位阶跃响应的过程。
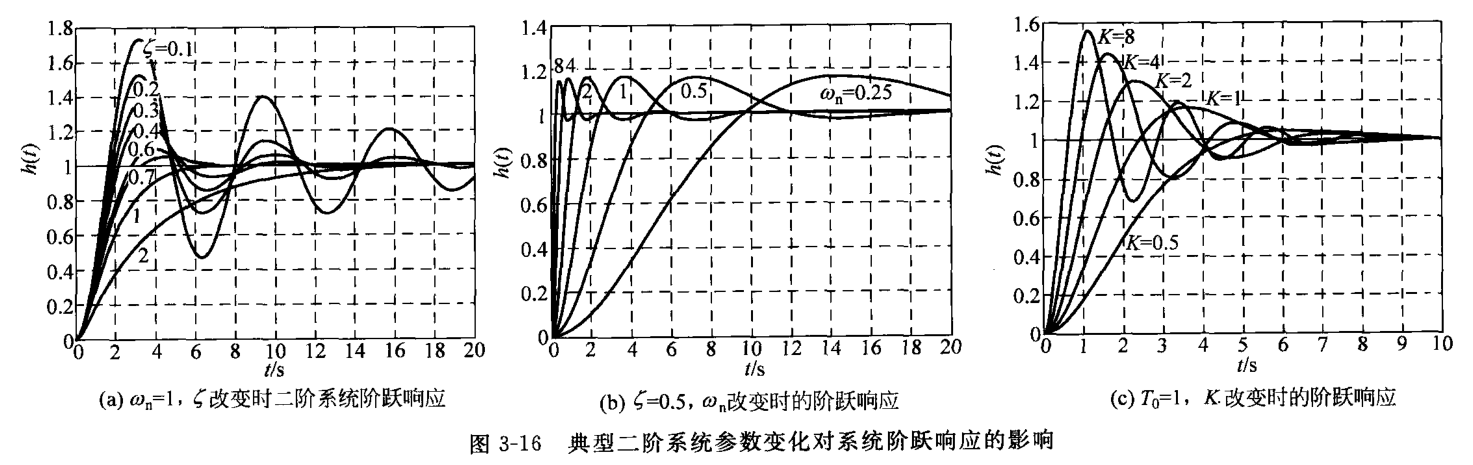
典型二阶系统参数变化对系统阶跃响应的影响(66页 图3-16)
从上面的讨论中我们可以看出,要获得满意的系统动态性能,应该适当选择参数,使二阶系统的闭环极点位于$\beta = 45 \degree$ 线附近,使系统具有合适的超调量,并根据情况尽量使其远离虚轴,以提高系统的快速性。
临界阻尼二阶系统的动态过程分析
当阻尼比 $\zeta = 1$ 时,系统处于临界阻尼状态。
临界阻尼二阶系统的闭环特征方程为
$$D(s) = s^2 + 2 \omega_\mathrm{n} s + \omega_\mathrm{n}^2 = 0 \ ,$$
从中可以解出一对相等的实特征根:
$$\lambda_1 = \lambda_2 = -\omega_\mathrm{n} = - \frac{1}{T_1} \ ,$$
此时系统单位阶跃响应的拉普拉斯变换为
$$C(s) = \varPhi(s) R(s) = \frac{\omega_\mathrm{n}^2}{(s + \omega_\mathrm{n})^2} \frac{1}{s} \ ,$$
对应的时域单位阶跃响应为
$$h(t) = 1 - (1 + \omega_\mathrm{n} t) \mathrm{e}^{- \omega_\mathrm{n} t} \ ,$$
临界阻尼系统的时域响应是一条单调上升的对数曲线,即临界阻尼系统不存在超调量。令 $h(t) = 0.95$ 可以解得 $5 \char37$ 误差带的调节时间
$$t_\mathrm{s} = 4.75 T_1 \ ,$$
即临界阻尼二阶系统的调节时间只与系统时间常数 $T_1$ 有关。在有些不允许时间响应出现超调,而又希望响应速度较快的场景中,例如在指示仪表系统和记录仪表系统中,需要采用临界阻尼系统。
过阻尼二阶系统的动态过程分析
当阻尼比 $\zeta > 1$ 时,系统处于过阻尼状态。
过阻尼二阶系统的闭环特征方程为
$$D(s) = s^2 + 2 \zeta \omega_\mathrm{n} s + \omega_\mathrm{n}^2 = 0 \ ,$$
从中可以解出一对不等的实特征根:
$$\lambda_{1, 2} = -\zeta \omega_\mathrm{n} \pm \omega_\mathrm{n} \sqrt{\zeta^2 - 1} \qquad \qquad \left ( \zeta > 1 \right ) $$
不妨设
$$ \lambda_1 = \frac{1}{T_1} = - (\zeta - \sqrt{\zeta^2 - 1} ) \omega_\mathrm{n} \qquad \lambda_2 = \frac{1}{T_2} = - (\zeta + \sqrt{\zeta^2 - 1} ) \omega_\mathrm{n} \qquad \qquad \left ( T_1 > T_2 \right ) $$
可得系统单位阶跃响应的拉普拉斯变换
$$C(s) = \varPhi(s) R(s) = \frac{\omega_\mathrm{n}^2}{(s + \frac{1}{T_1})(s + \frac{1}{T_2})} \frac{1}{s} \ ,$$
反变换回时域,得到系统的时域单位阶跃响应
$$h(t) = 1 + \frac{e^{-\frac{t}{T_1}}}{\frac{T_2}{T_1} - 1} + \frac{e^{-\frac{t}{T_2}}}{\frac{T_1}{T_2} - 1} \qquad \qquad \left ( t \geq 0 \right)$$
过阻尼二阶系统单位阶跃响应也是无振荡的单调上升曲线,同样不存在超调量。令 $\dfrac{T_1}{T_2}$ 取不同的值,可以分别求解对应的无量纲调节时间 $\dfrac{t_\mathrm{s}}{T_1}$ 如下图所示。
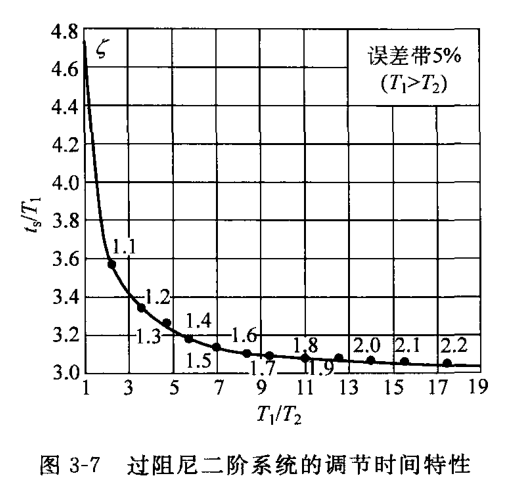
过阻尼二阶系统的调节时间特性(66页 图3-7)
上图中的 $\zeta$ 为参变量,由系统特征方程
$$D(s) = s^2 + 2 \zeta \omega_\mathrm{n} s + \omega_\mathrm{n}^2 = (s + \frac{1}{T_1})(s + \frac{1}{T_2}) = 0$$
可以解得
$$\zeta = \frac{1 + \frac{T_1}{T_2}}{2 \sqrt{\frac{T_1}{T_2}}} \ ,$$
当 $\dfrac{T_1}{T_2}$(或 $\zeta$)很大时,特征根 $\lambda_2 = \dfrac{1}{T_2}$ 比 $\lambda_1 = \dfrac{1}{T_1}$ 远离虚轴,其所对应模态 $\mathrm{e}^{-\frac{t}{T_2}}$ 很快衰减为零,系统调节时间主要由 $\lambda_1$ 对应的模态 $\mathrm{e}^{-\frac{t}{T_1}}$ 决定。此时可将过阻尼二阶系统近似看作由 $\lambda_1$ 确定的一阶系统,估算其动态性能指标。上图中的曲线体现了这一规律性。
卢老师的书中还提及了对二阶系统附加闭环零极点的时域分析。此段内容比较长而且并不如根轨迹分析来得直观,故在本文中跳过了这部分。
高阶系统的时域分析
这部分内容主要来自卢京潮《自动控制原理》第3章 线性系统的时域分析与校正 3.4 高阶系统的阶跃响应及动态性能。
在进入高阶系统的时域分析前,我们先引入主导极点的概念。
闭环主导极点
这部分内容可以参考胡寿松 《自动控制原理(第七版)》 102页 高阶系统闭环主导极点及其动态性能分析。
对稳定的闭环系统,远离虚轴的极点对应的模态因为收敛较快,只影响阶跃响应的起始段,而距虚轴近的极点对应的模态衰减缓慢,系统动态性能主要取决于这些极点对应的响应分量。此外,各瞬态分量的具体值还与其系数大小有关。
根据部分分式理论,各瞬态分量的系数与零、极点的分布有如下关系:
若某极点远离原点,则相应项的系数很小;
若某极点接近一零点,而又远离其他极点和零点,则相应项的系数也很小;
若某极点远离零点又接近原点或其他极点,则相应项系数就比较大。
系数大而且衰减慢的分量在瞬态响应中起主要作用。因此,距离虚轴最近而且附近又没有零点的极点对系统的动态性能起主导作用,称相应极点为主导极点。
为了使高阶系统的性能尽量优秀,一般会通过调整增益使得系统具有一对共轭的闭环主导极点4,从而可以使用二阶系统的动态性能指标估算高阶系统的动态性能。一般规定,若某极点的实部大于主导极点实部的5~6倍以上时,则可以忽略相应分量的影响;若两相邻零、极点间的距离比它们本身的模值小一个数量级(10倍以上)时,则称该零、极点对为“偶极子”,其作用近似抵消,可以忽略相应分量的影响。
但二阶近似并不能完全反映高阶系统的动态性能,额外的零/极点将会带来如下影响:
闭环零点影响:闭环零点的存在会减小峰值时间,使系统响应速度加快,超调量 $\sigma \char37$ 增大。这表明闭环零点会减小系统阻尼,并且这种作用将随闭环零点接近虚轴而加剧。因此,配置闭环零点时,要折中考虑闭环零点对系统响应速度和阻尼程度的影响。
闭环非主导极点影响:非主导极点会增大峰值时间,使系统响应速度变缓,但可以使超调量 $\sigma \char37$ 减小。这表明闭环非主导极点可以增大系统阻尼,且这种作用将随极点接近虚轴而加剧。
有关高阶系统中零极点位置对系统性能的影响将会在 下一篇文章 中展开具体讨论;此外还可以参考下面的 估算高阶系统动态性能指标的零点极点法。
高阶系统的单位阶跃响应
现在我们来讨论高阶系统在时域上的单位阶跃响应,其实就是在 $s$ 域中求解代数方程后反变换回时域从而得到系统时域微分方程的解。
高阶系统的传递函数一般可以表示为
$$ \begin{aligned} \varPhi (s) &= \frac{M(s)}{D(s)} = \frac{b_m s^m + b_{m - 1} s^{m - 1} + … + b_1 s + b_0}{a_n s^n + a_{n - 1} s^{n - 1} + … + a_1 s + a_0} \newline &= \frac{\displaystyle K \prod_{i=1}^{m} (s - z_i)}{\displaystyle \prod_{j=1}^{q} (s - \lambda_j) \prod_{k=1}^{r} (s^2 + 2 \zeta_k \omega_k s + \omega_k^2)} \qquad \qquad \left ( n \geq m \right) \end{aligned} $$
此处假设所研究的高阶系统有 $q$ 个闭环实极点与 $r$ 对闭环共轭复极点,及 $m$ 个闭环实零点。拥有更多复极点/复零点的系统也可以类似的形式分析。
上式中 $K = \frac{b_m}{a_n} , q + 2r = n \ .$ 由于 $M(s)$ 和 $D(s)$ 均为实系数多项式,故闭环零点 $z_i$、极点 $\lambda_j$ 只能是实根或共轭复根。系统单位阶跃响应的拉普拉斯变换可表示为
$$ \begin{aligned} C(s) &= \varPhi(s) \frac{1}{s} = \frac{\displaystyle K \prod_{i=1}^{m} (s - z_i)}{s \displaystyle \prod_{j=1}^{q} (s - \lambda_j) \prod_{k=1}^{r} (s^2 + 2 \zeta_k \omega_k s + \omega_k^2)} \newline &= \frac{A_0}{s} + \sum_{j=1}^{q} \frac{A_j}{s - \lambda_j} + \sum_{k=1}^{r} \frac{B_k s + C_k}{s^2 + 2 \zeta_k \omega_k s + \omega_k^2} \end{aligned} $$
式中 $A_0 = \displaystyle \lim_{s \to 0} s C(s) = \frac{M(0)}{D(0)}, A_j = \lim_{s \to j} (s - \lambda_j) C(s)$ 是 $C(s)$ 在闭环实极点 $\lambda_j$ 处的留数5; $B_k$ 和 $C_k$ 是 $C(s)$ 在闭环复极点 $- \zeta_k \omega_k \pm \mathrm{j} \omega_k \sqrt{1 - \zeta_k^2}$ 处的留数有关的常系数。对上式做拉普拉斯反变换可得
$$c(t) = A_0 + \sum_{j=1}^{q} A_j \cdot \mathrm{e}^{\lambda_j t} + \sum_{k=1}^r D_k \cdot \mathrm{e}^{- \sigma_k t} \sin (\omega_{\mathrm{d} k} t + \varphi_k)$$
式中 $D_k$ 是 $C(s)$ 在闭环复极点 $- \zeta_k \omega_k \pm \mathrm{j} \omega_k \sqrt{1 - \zeta_k^2}$ 处的留数有关的常系数
$$\sigma_k = \zeta_k \omega_k, \qquad \omega_{\mathrm{d} k} = \omega_k \sqrt{1 - \zeta_k^2} \ .$$
从上面的讨论可以看出除常数项 $A_0 = \frac{M(0)}{D(0)}$ 外,高阶系统的单位阶跃响应是系统模态的组合,组合系数即部分分式系数。
模态由闭环极点确定,而部分分式系数与闭环零点、极点分布有关,所以,闭环零点、极点对系统动态性能均有影响。当所有闭环极点均具有负的实部,即所有闭环极点均位于左半 $s$ 平面时,随时间 $t$ 的增加所有模态均趋于零(对应瞬态分量),系统的单位阶跃响应最终稳定在 $\frac{M(0)}{D(0)}$。很明显,闭环极点负实部的绝对值越大,相应模态趋于零的速度越快。在系统存在重根的情况下,以上结论仍然成立。
这里相当于复述了一遍我们在前两篇文章讨论拉普拉斯变换和系统微分方程/传递函数的关系时所得到的结论。
估算高阶系统动态性能指标的零点极点法
在绝大多数实际系统的闭环零、极点中,可以选留最靠近虚轴的一个或几个极点作为主导极点,略去比主导极点距虚轴远5倍以上的闭环零、极点,以及不十分接近虚轴的相互靠得很近的偶极子,忽略其对系统动态性能的影响,然后按下表中相应的公式估算高阶系统的动态性能指标。
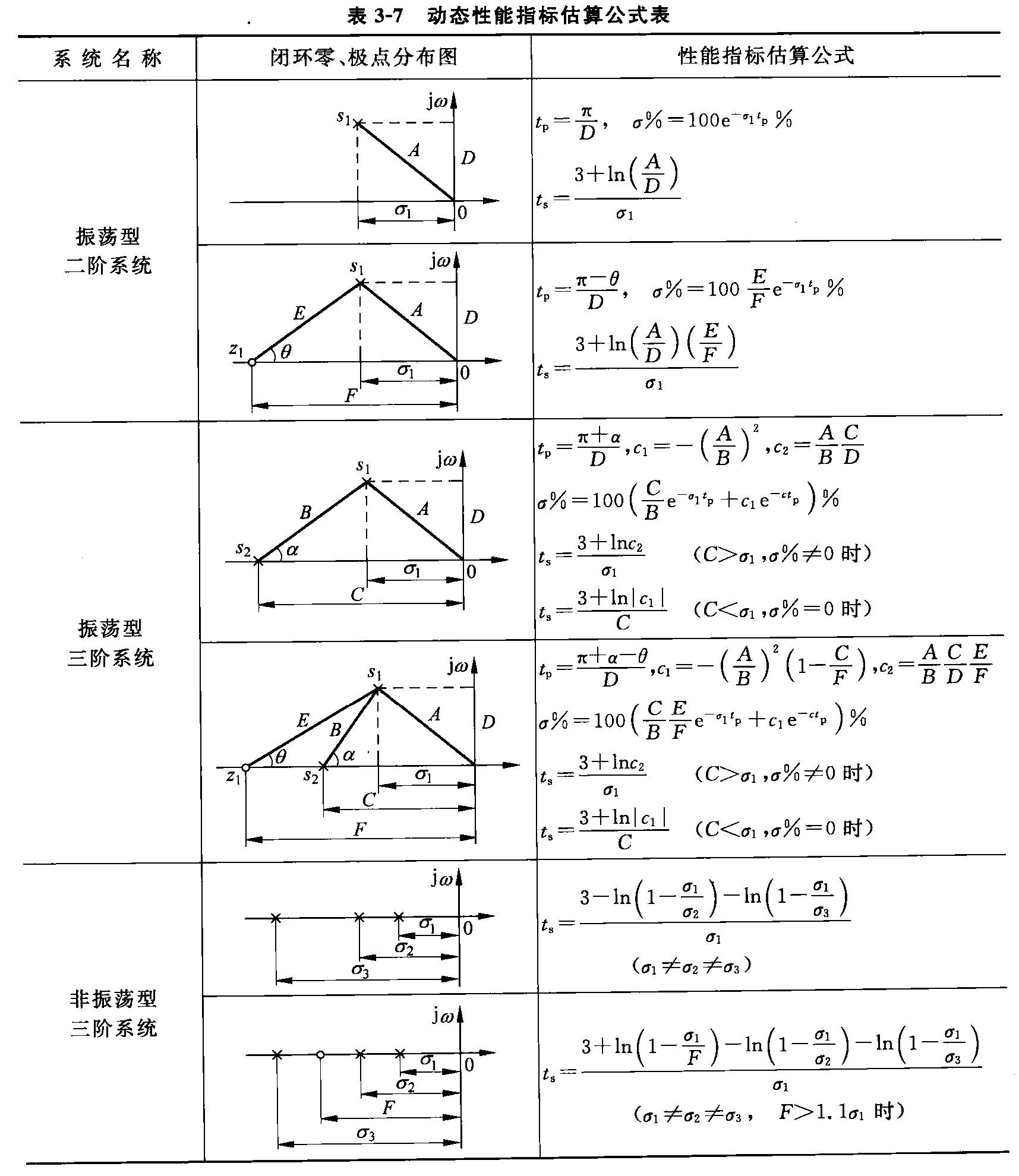
动态性能指标估算公式表(78页 图3-7)
线性系统的稳定性分析
我们在初识自动控制原理时已经介绍了一个良好的控制系统应当满足的三大特性:稳、准、快。其中稳是对系统的基本要求。
稳定性的概念
如果在扰动作用下系统偏离了原来的平衡状态,当扰动消失后,系统自身能够以足够的准确度恢复到原来的平衡状态,则系统是稳定的;否则,系统不稳定。
稳定的充要条件
先给出结论:对于从系统特征方程 $D(s) = 0$ 解得的特征根,无论是实根还是共轭复根,所有特征根都具有负的实部是系统稳定的充分必要条件。
考虑零极点形式的系统闭环传递函数
$$\varPhi(s) = \frac{M(s)}{D(s)} = \frac{b_m s^m + b_{m - 1} s^{m - 1} + … + b_1 s + b_0}{a_n s^n + a_{n - 1} s^{n - 1} + … + a_1 s + a_0} \ ,$$
我们先讨论闭环极点为互不相同的单根的情形。此时有
$$\varPhi(s) = \frac{A_1}{s - \lambda_1} + \frac{A_2}{s - \lambda_2} + … + \frac{A_n}{s - \lambda_n} = \sum_{i=1}^{n} \frac{A_i}{s - \lambda_i} \ ,$$
式中 $A_i = \displaystyle \lim_{s \to \lambda_i} (s - \lambda_i) C(s)$ 是 $C(s)$ 在闭环极点 $\lambda_i$ 处的留数。对上式进行拉普拉斯反变换,得系统的单位脉冲响应函数6
$$k(t) = A_1 \mathrm{e}^{\lambda_1 t} + A_2 \mathrm{e}^{\lambda_2 t} + … + A_n \mathrm{e}^{\lambda_n t} = \sum_{i=1}^n A_i \mathrm{e}^{\lambda_i t} \ ,$$
根据稳定性的定义,系统稳定时应该有
$$\lim_{t \to \infty} k(t) = \lim_{t \to \infty} \sum_{i=1}^{n} A_i \mathrm{e}^{\lambda_i t} = 0 \ ,$$
由于留数 可能取得任意值,为使上式成立,则必有
$$\lim_{t \to \infty} \mathrm{e}^{\lambda_i t} = 0 \qquad \left ( i = 1, 2, …, n \right )$$
不难看出:如系统的所有特征根均具有负的实部,则上式成立,反之亦然。
对于存在 $l$ 重根的系统,假设重根为 $\lambda_0 \ ,$ 则相应模态
$$\mathrm{e}^{\lambda_0 t}, t \mathrm{e}^{\lambda_0 t}, t^2 \mathrm{e}^{\lambda_0 t}, …, t^{l-1} \mathrm{e}^{\lambda_0 t}$$
在时间 $t$ 趋于无穷大时是否收敛到零,仍然取决于重特征根 $\lambda_0$ 是否具有负的实部。
当系统有纯虚根时,系统处于临界稳定状态,脉冲响应呈现等幅振荡。由于系统参数的变化以及扰动是不可避免的,实际上等幅振荡不可能永远维持下去,系统很可能会由于某些因素而导致不稳定。另外,从工程实践的角度来看,这类系统也不能正常工作,因此经典控制理论中将临界稳定系统划归到不稳定系统之列。
线性系统的稳定性是其自身的属性,只取决于系统自身的结构、参数,与初始条件及外作用无关。
线性定常系统如果稳定,则它一定是大范围稳定7的,且原点是其唯一的平衡点。
稳定判据
设系统的特征方程为
$$D(s) = a_n s^{n} + a_{n-1} s^{n-1} + … + a_1 s + a_0 = 0 \qquad \qquad (a_n > 0)$$
则系统稳定的必要条件是
$$a_i > 0 \qquad \qquad (i = 0, 1, 2, …, n)$$
满足必要条件的一、二阶系统一定稳定。但对于高阶系统,单纯满足必要条件不一定稳定,还需要使用劳斯-赫尔维茨稳定性判据。
劳斯-赫尔维茨判据
劳斯判据需要列出如下格式的劳斯表。表的索引列为从 $s$ 的最高次幂 $s^n$ 逐次降低到 $s^0$ ;前两行分别由特征方程奇/偶项系数构成,其他各行根据前两行的数值计算。

劳斯表(81页 图3-8)
劳斯表中从第 $n-2$ 行开始,系数根据前两行的数值计算。例如对于第 $n-3$ 行、第 $2$ 列,其数值为上一行($n-2$)的第 $1$ 列乘上二行($n-1$)的第 $3$ 列,再减去上二行的第 $1$ 列乘上一行的第 $3$ 列后,所得的差除以上一行的第 $1$ 列所得结果,其分子的计算过程有点类似于二阶行列式的反向顺序,分母则总是取上一行的第 $1$ 列。
在得到劳斯表后,我们可以根据其中的两个特征判断系统的稳定性:
系统稳定的充分必要条件是劳斯表中第一列的系数都大于 $0$ ;
劳斯表第一列符号改变的次数就是系统特征方程对应具有正实部的根的个数。
劳斯判据特殊情况的处理
劳斯表计算过程中有时会得到某行的第一列元素为 $0 \ ,$ 若按原规则计算下一行会出现除零的情况。此时可以用一个符号 $\epsilon$ 代替 $0$ 参与计算并列出代数式,最后计算各个算式取 $\epsilon \to 0$ 的极限过程时的结果得到劳斯表。

存在第一列元素为 $0$ 时劳斯表的计算(82页 例3-11)
在另一种情况下,劳斯表中某行元素可能全部为零,此时需利用上一行元素构成辅助方程。辅助方程为根据上一行各参数及其索引列 $s^i$ 阶数 $i$ 隔阶列写的代数方程,对辅助方程求导得到新的方程,用新方程的系数代替该行的零元素继续计算。

存在全为 $0$ 的行时劳斯表的计算(82页 例3-12)
当系统中存在关于实轴对称的极点对时,也即当特征多项式包含形如 $(s + \sigma) (s - \sigma)$ 或 $(s + \mathrm{j} \omega) (s - \mathrm{j} \omega)$ 的因子时,劳斯表会出现全零行,而此时辅助方程的根就是特征方程根的一部分,也是系统中存在的对称于原点的特征根。
使用劳斯判据判断系统稳定的参数范围
由于劳斯判据本质是一种经过严格证明的、用于判断一个多项式方程中是否存在位于复平面右半部的正根的数学工具,于是我们可以通过对原系统特征方程进行变换后求解的方式来利用劳斯判据判断一组参数是否能使系统稳定。
例:假设单位负反馈系统的开环传递函数为
$$G(s) = \frac{K_a}{s(s^2 + 20 \zeta s + 100)} \ ,$$
确定当 $\zeta = 2$ 时使系统极点全部落在直线 $s = 1$ 左边的 $K$ 范围。
解:
由上式可以得到系统的开环增益(尾1型具有的常数项增益)为 $K = \dfrac{K_a}{100} \ ,$ 并可得系统特征方程
$$D(s) = s^3 + 20 \zeta s^2 + 100 s + 100 K = s^3 + 40 s^2 + 100 s + 100 K = 0 \ ,$$
作坐标变换 $s = \hat{s} - 1$ 使新坐标的虚轴 $\hat{s} = 0 \ ,$ 就可以在新坐标系下用劳斯判据解决问题。令
$$ \begin{aligned} D(\hat{s}) &= (\hat{s} - 1)^3 + 40 (\hat{s} - 1)^2 + 100(\hat{s} - 1) + 100K \newline &= \hat{s}^3 + 37 \hat{s}^2 + 23 \hat{s} + (100K - 61) \end{aligned} $$
可得劳斯表
$$ \begin{matrix} \hat{s}^3 & 1 & 23 & \newline \newline \hat{s}^2 & 37 & 100K - 61 & \newline \newline \hat{s}^1 & \dfrac{37 \times 23 + 61 - 100K}{37} & 0 & \to K < 9.12 \newline \newline \hat{s}^0 & 100K - 61 & 0 & \to K > 0.61 \end{matrix} $$
为使新的、使用 $\hat{s}$ 的系统稳定,劳斯表中第一列的元素应全大于 $0 \ ,$ 从而得系统开环增益 $K$ 应满足 $0.61 < K < 9.12 \ .$
线性系统的稳态误差
劳斯稳定判据解决的是系统绝对稳定性的问题。在系统设计时,往往不仅需要知道系统是否绝对稳定,而且需要知道系统稳定的程度,即一个稳定的控制系统距临界稳定状态还有多大的裕度(或称稳定裕度)。
控制系统的稳态误差是系统控制精度的一种度量,是系统的稳态性能指标。由于系统自身的结构参数、外作用的类型(控制量或扰动量)以及外作用的形式(阶跃、斜坡或加速度等)不同,控制系统的稳态输出不可能在任意情况下都与输入量(希望的输出)一致,因而会产生原理性稳态误差。此外,系统中存在的不灵敏区、间隙、零漂等非线性因素也会造成附加的稳态误差。控制系统设计的任务之一,就是尽量减小系统的稳态误差。
对稳定的系统研究稳态误差才有意义,所以计算稳态误差应以系统稳定为前提。
误差的输入端定义与输出端定义
我们之前提到,线性系统一般有两种定义误差的方式:输入端定义和输出端定义。
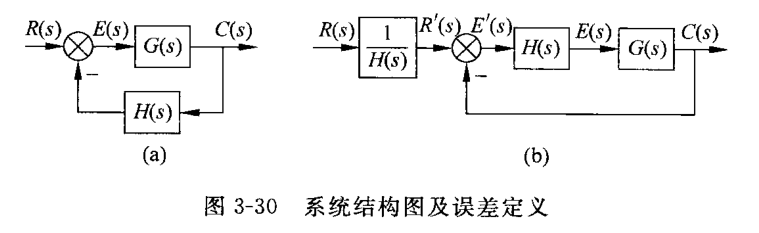
典型系统结构图(85页 图3-30)
参考上图(a), 按输入端定义的误差(即把偏差定义为误差)为
$$E(s) = R(s) - H(s)C(s) \ ,$$
按输出端定义的误差为
$$E^{\prime} (s) = \frac{R(s)}{H(s)} - C(s) \ ,$$
按输入端定义的误差 $E(s)$(即偏差)通常是可测量的,有一定的物理意义,但其误差的理论含义不十分明显;按输出端定义的误差 $E^{\prime} (s)$ 是“希望输出” $R^{\prime} (s)$ 与实际输出 $C(s)$ 之差,比较接近误差的理论意义,但它通常不可测量,只有数学意义。两种误差定义之间存在如下关系
$$E^{\prime} (s) = \frac{E(s)}{H(s)} \ .$$
特别地,对单位反馈系统,上述两种定义方式的误差是一致的。
计算稳态误差的一般方法
前面我们将输入信号 $R(s)$ 减去主反馈通路的反馈信号 $B(s)$ 得到的偏差 $E(s)$ 为系统误差。在此定义下,计算系统在稳态状态下的误差即为计算 $E(s)$ 对应的时域变量 $e(t)$ 在 $t \to \infty$ 时的值,可通过终值定理求得;具体的计算分为三步。
判定系统的稳定性。稳定是系统正常工作的前提条件,系统不稳定时,求稳态误差没有意义。
按需求取控制输入/扰动输入作用下的闭环误差传递函数 $\varPhi_\mathrm{e} (s)$ 与 $\varPhi_\mathrm{en} (s)$
$$\varPhi_\mathrm{e} (s) = \frac{E(s)}{R(s)}, \qquad \varPhi_\mathrm{en} (s) = \frac{E(s)}{N(s)} ,$$
- 用终值定理求稳态误差
$$e_\mathrm{ss} = \lim_{s \to 0} s \left [ \varPhi_\mathrm{e} (s) R(s) + \varPhi_\mathrm{en} (s) N(s) \right ] \ .$$
静态误差系数法
含积分环节 的系统在典型输入作用下的稳态误差的求取可以归纳总结为静态误差系数法。
对于结构类似 图3-30 的系统,其开环传递函数一般可以表示为
$$G(s)H(s) = \frac{K (\tau_1 s + 1)(\tau_2 s + 1) … (\tau_m s + 1)}{s^v (T_1 s + 1)(T_2 s + 1) … (T_{n-v} s + 1)} = \frac{K}{s^v} G_0 (s) \ ,$$
式中 $G_0 (s) = \dfrac{K (\tau_1 s + 1)(\tau_2 s + 1) … (\tau_m s + 1)}{s^v (T_1 s + 1)(T_2 s + 1) … (T_{n-v} s + 1)} \ ,$ 有 $\lim_{s \to 0} G_0 (s) = 1 \ ;$ $K$ 是开环增益;$v$ 是系统开环传递函数中纯积分环节的个数,称为系统型别,也称为系统的无差度。
无差系统是指在阶跃输入作用下不存在稳态误差的系统。
当 $v = 0$ 时,相应闭环系统为 $0$ 型系统,也称为“有差系统”。
当 $v = 1$ 时,相应闭环系统为 $\mathrm{I}$ 型系统,也称为“一阶无差系统”。
当 $v = 2$ 时,相应闭环系统为 $\mathrm{II}$ 型系统,也称为“二阶无差系统”。
在控制输入作用下,系统的误差传递函数可写为
$$\varPhi_\mathrm{e} (s) = \frac{E(s)}{R(s)} = \frac{1}{1 + G(s) H(s)} = \frac{1}{1 + \frac{K}{s^v} G_0 (s)}$$
阶跃(位置)输入时,$r(t) = A \times 1(t)$
$$e_\mathrm{ssp} = \lim_{s \to 0} s \varPhi_\mathrm{e} (s) R(s) = \lim_{s \to 0} \frac{A}{s} \frac{1}{1 + G(s) H(s)} = \frac{A}{1 + \lim_{s \to 0} G(s) H(s)} \ ,$$
定义静态位置(position)误差系数
$$K_\mathrm{p} = \lim_{s \to 0} G(s) H(s) = \lim_{s \to 0} \frac{K}{s^v} \ ,$$
则系统的稳态位置误差
$$e_\mathrm{ssp} = \frac{A}{1 + K_\mathrm{p} } \ ,$$
上式即为系统在单位阶跃输入时产生的时域误差表达式。
类似地,可以定义系统在斜坡(速度)输入 $r(t) = A t$ 时的静态速度(velocity)误差系数与相应的稳态速度误差
$$K_\mathrm{v} = \lim_{s \to 0} \frac{K}{ s^{\mathrm{v} - 1} }, \qquad e_\mathrm{ssv} = \frac{A}{ K_\mathrm{v} }; $$
以及加速度(acceleration)输入 $r(t) = \dfrac{A}{2} t^2$ 时的静态加速度误差系数与稳态加速度误差
$$K_\mathrm{a} = \lim_{s \to 0} \frac{K}{ s^{\mathrm{v} - 2} }, \qquad e_\mathrm{ssa} = \frac{A}{ K_\mathrm{a} }. $$
综合以上讨论可得到下表

典型输入信号作用下的稳态误差(88页 表3-9)
上表揭示了控制输入作用下,系统稳态误差随系统结构、参数及输入形式变化的规律。在输入一定时,增大开环增益 $K$,可以减小稳态误差;增加开环传递函数中的积分环节数 $v$,可以消除稳态误差。更具体地,对于 $n$ 型系统,时域上小于 $n$ 次的控制输入信号 $r(t) = \dfrac{1}{k!} t^k$ 产生的稳态误差总是为$0$.
动态误差系数法
TODO: 补充完成动态误差系数法
当 $T$ 越小时,$\mathrm{e}^{- \frac{t_\mathrm{s}}{T}}$ 的指数部分的绝对值就会越大,对应使 $\mathrm{e}^{- \frac{t_\mathrm{s}}{T}}$ 收敛速度更快。 ↩︎
我个人比较喜欢把 $\mathrm{e}^{-\zeta \omega_\mathrm{n} t}$ 记作 $\mathrm{e}^{-t \sin \beta} \ ,$ $\mathrm{e}^{-\frac{\zeta}{\sqrt{1 - \zeta^2}} \pi}$ 记作 $\mathrm{e}^{-\pi \cot \beta} \ ,$ $\sqrt{1 - \zeta^2} \omega_\mathrm{n}$ 记作 $\omega_d \ ,$ 因为比较容易记住 :D ↩︎
可以证明,对于一般的实系数线性控制系统(所有物理量、元件参数为实数),其复平面上的极点 / 零点总是成对出现。 ↩︎
传递函数的拉普拉斯反变换即为系统的脉冲响应(即系统在单位脉冲信号 $\delta(t)$ 激励下产生的输出)。 ↩︎
相对于对非线性系统做 小偏差线性化 后求解出的系统参数只在所研究的工作点附近准确,线性定常系统在参数变化的一个较大范围内都具有稳定性。 ↩︎